图的基本介绍
什么是图
图(graph)是一种非线性的数据结构,由顶点(vertex)和边(edge)组成。
顶点和边的集合:
V ={1,2,3,4,5}
E = {(1,2), (1,3), (2,5), (3,4), (4,5)}
转换数学模型:
G = {V, E}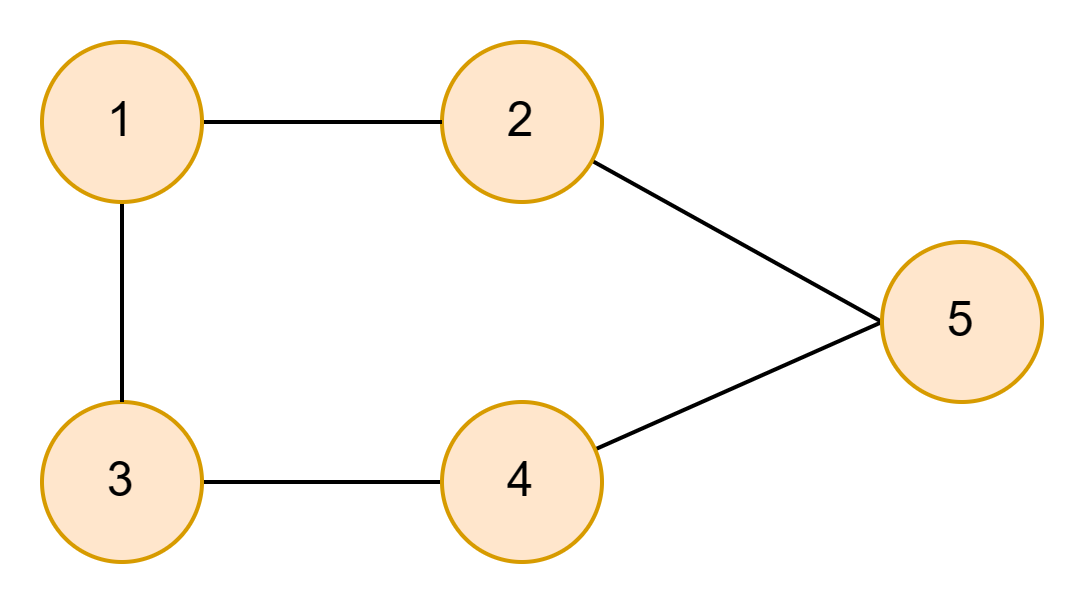
相较于线性关系(链表)和分治关系(树),网络关系(图)的自由度更高,因此也更复杂。
图的常见类型和术语
常见类型
无向图(undirected graph)
有向图(directed graph)
连通图(connected graph)
非连通图(disconnected graph)
有权图(weighted graph)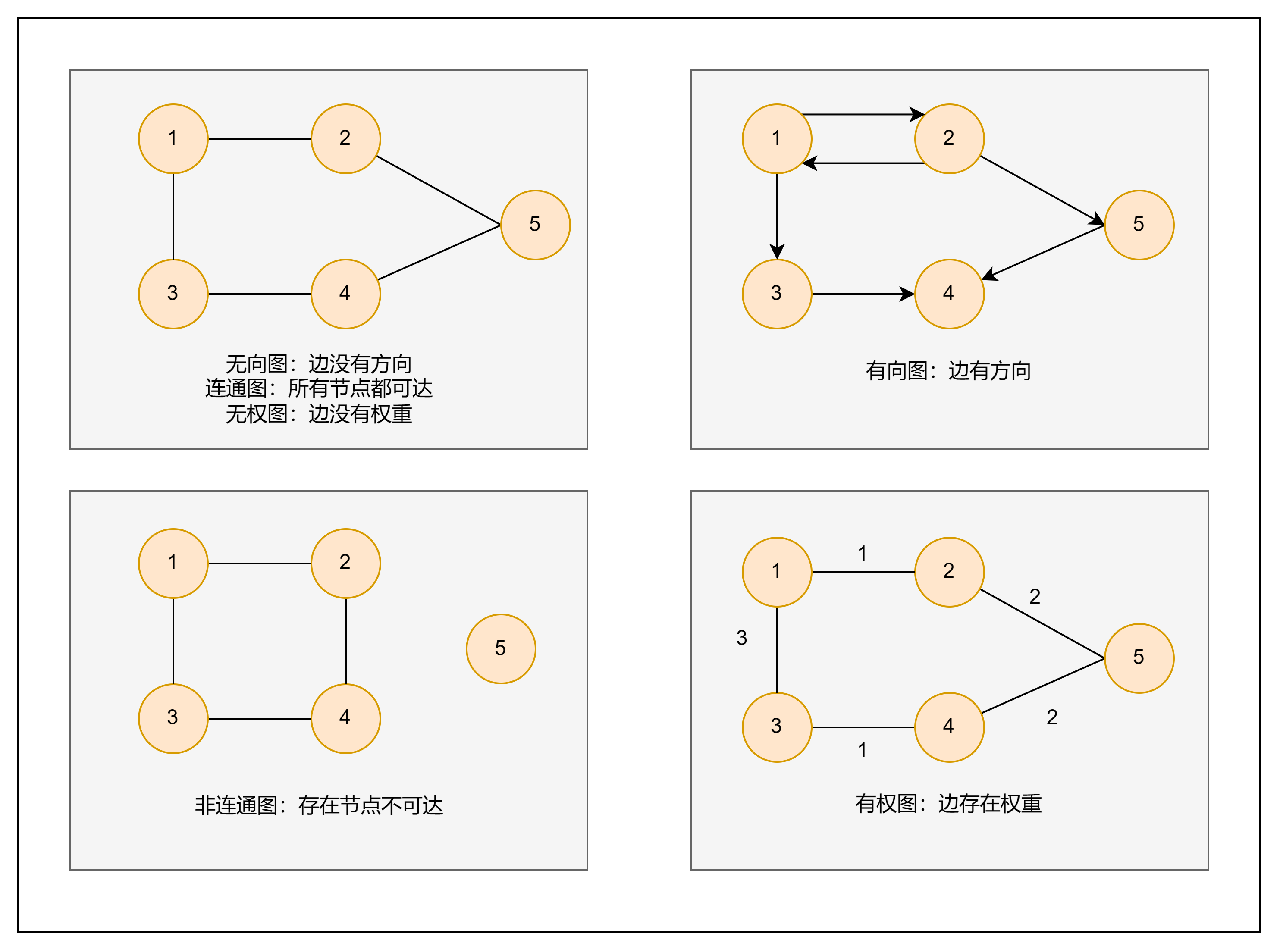
常用术语
邻接(adjacency):当顶点之前存在边相连,则称这两顶点邻接
路径(path):从顶点1到顶点5所经过的边构成序列被称为从1到5的路径
度(degree):一个顶点拥有的边数。针对有向图,还存在in-degree多少边指向该点,out-degree多少边从该点指出。
图的表示
邻接矩阵
设图的顶点数量为n,邻接矩阵(adjacency matrix)使用nxn大小的矩阵来表示图,每一行代表一个顶点,矩阵元素代表边,用1或0表示顶点是否存在边。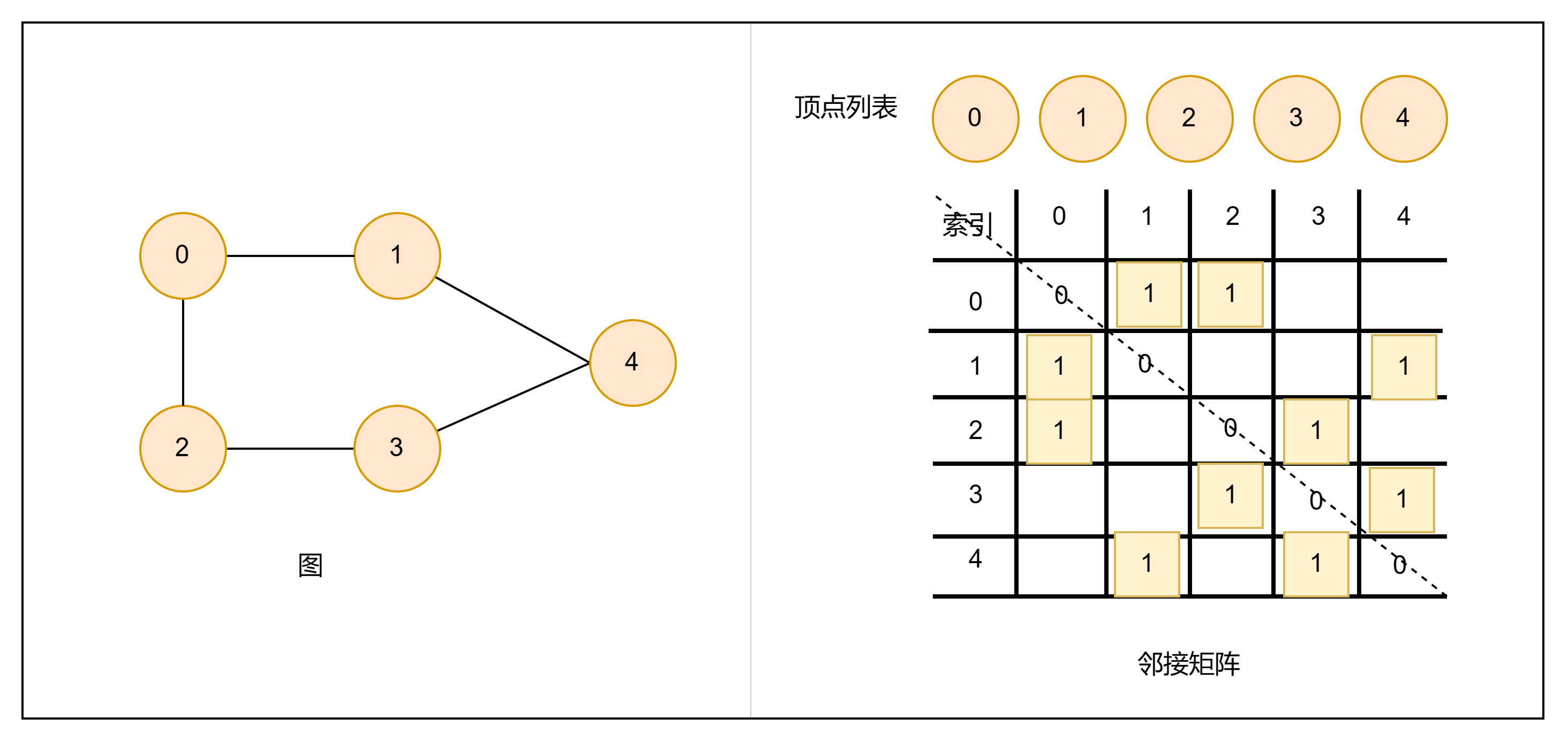
邻接矩阵特性:
- 顶点不能与自身相连,因此邻接矩阵的对角线元素没有意义
- 对于无向图,两个方向等价,此时邻接矩阵关于主对角线对称
- 将邻接矩阵的元素由1或0替换为权重,则可表示有权图
使用邻接矩阵,我们可以直接访问矩阵元素获取边,因此增删改查效率高,时间复杂度O(1), 但空间复杂度较高O(n^2)。
邻接表
邻接表(adjacency list)使用n个链表表示图,链表节点表示顶点。第i个链表表示第i个节点,其中存储了该顶点的所有邻接顶点(与该顶点相连的顶点)。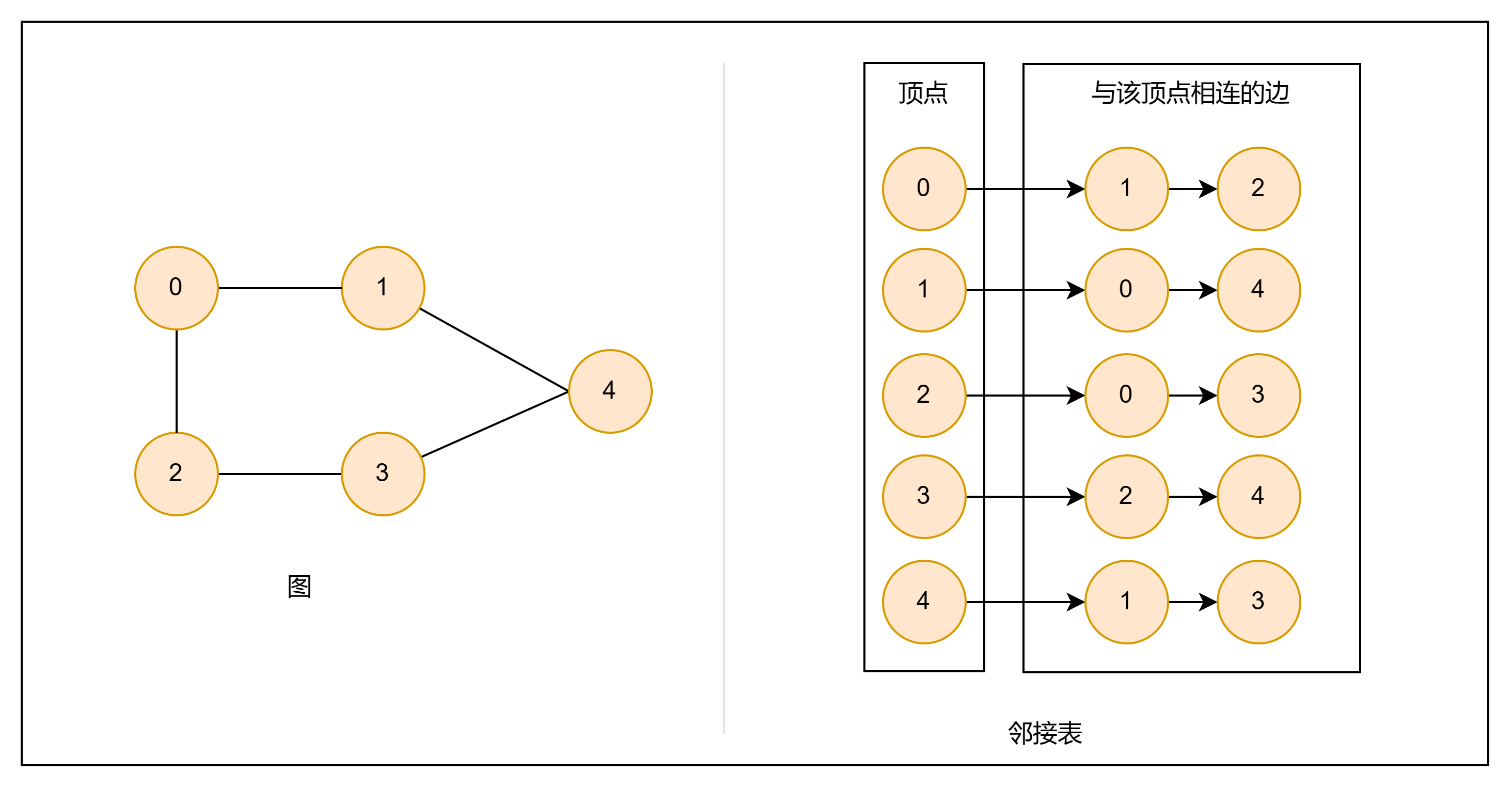
邻接表存储空间只存实际存在的边,远小于n^2。空间小,但需要通过遍历链表查找,时间效率不如邻接矩阵。
可以将邻接表类比哈希表,实现优化。链表转为AVL树或红黑树,时间复杂度由O(n)->O(logn);还可以直接转为哈希表,将时间复杂度降低到O(1)。
图的一般应用
许多现实问题可以使用图建模,和通过图计算解决相应问题
| 现实场景 | 顶点 | 边 | 图计算问题 |
|---|---|---|---|
| 社交网络 | 用户 | 好友关系 | 潜在好友推荐 |
| 地铁线路 | 站点 | 站点间的连通 | 最短路线推荐 |
| 互联网 | 路由节点 | 路由之间的连接 | 最对路由路径推荐 |